Raúl Rojas González es profesor en el Departamento de Matemáticas y Computación de la Universidad Libre de Berlín. Es egresado del Instituto Politécnico Nacional donde obtuvo sus grados de licenciatura y maestría en matemáticas. Posteriormente realizó estudios de doctorado y obtuvo la habilitación en Ciencias de la Computación en la Universidad Libre de Berlín.  Es Premio Nacional de Ciencias y Artes 2015 y actualmente es profesor emérito de Inteligencia Artificial de la Universidad Libre de Berlín.

Esta publicación fue revisada por el comité editorial de la Academia de Ciencias de Morelos.

Ajedrez y fútbol

Este fin de semana pasado comenzó el Mundial de Fútbol en Qatar y ya millones de entrenadores de sofá en todo el orbe están listos para vociferarle a la televisión, apoyando o bien lamentando a su equipo. Claro, todos quisiéramos tener una bola de cristal en las manos, que nos revele ya cuál equipo resultará triunfador. En ausencia de algo así tenemos que recurrir a la simulación con ayuda de una computadora, cual oráculo moderno. ¿Pero cómo se simula un torneo de fútbol?

Lo primero que se necesita es una estimación de la potencia futbolística de cada equipo. Para ello existen los rankings de la FIFA o bien el escalafón Elo, tomado del ajedrez y trasladado al fútbol. El sistema Elo le asigna puntos a cada equipo de tal manera que, de la diferencia de puntos entre dos selecciones, se puede calcular la probabilidad de que cada una de ellas gane o pierda el encuentro. Por ejemplo, equipos con el mismo número de puntos Elo son igualmente potentes y un juego entre ambos equivale a tirar una moneda al aire. Pero un equipo 100 puntos Elo por encima de otro, tiene una probabilidad de 64% de ganar un partido entre ambas escuadras. La curva en la figura 1 muestra como la probabilidad de ganar un partido (eje vertical) aumenta hacia la derecha, para un equipo con la diferencia de puntos Elo mostrada en el eje horizontal. Para equipos con menos puntos Elo, es decir, una diferencia negativa, su probabilidad de ganar disminuye hacia la izquierda de la curva.

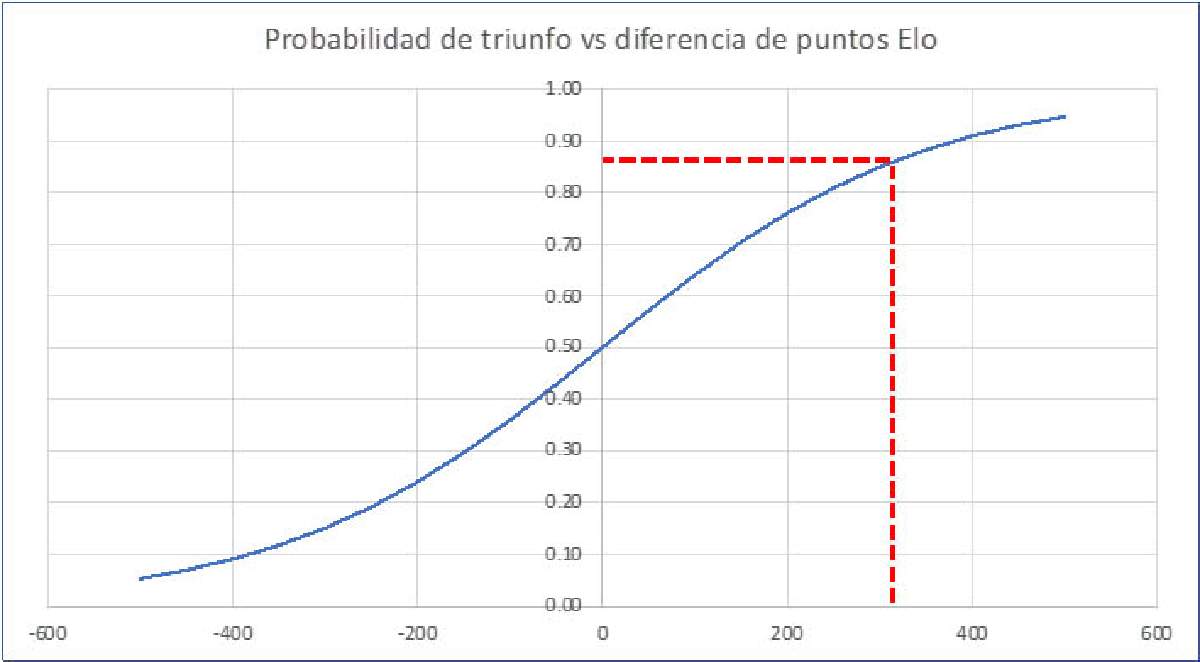
Figura 1. La curva de probabilidad de ganar un partido de fútbol de acuerdo con el puntaje Elo. La línea roja muestra, para una diferencia de 339 puntos Elo, que la probabilidad de ganar es de 87% para la escuadra más fuerte.

En el más reciente escalafón Elo, a Brasil, por ejemplo, se le han asignado 2160 puntos y 1821 a México. La diferencia es de 339 puntos, un poco apabullante. Por eso, de acuerdo con la fórmula Elo, la actual selección de Brasil debería ganar el 87% de los partidos contra el aguerrido pero inofensivo equipo del Tata Martino. La línea roja muestra la diferencia de puntos y la probabilidad correspondiente.

Ahora bien, lo que importa son los goles que se anotan en un juego. Ya que los goles caen a cuentagotas, apenas 2.6 en promedio durante el Mundial de 2018, se trata de un fenómeno poco frecuente y por eso se puede modelar con lo que en la estadística se llama la distribución de Poisson. Esta distribución matemática ha sido llamada la “ley de los pequeños números”, ya que modela la ocurrencia de eventos que suceden esporádicamente, como los terremotos. Es una ironía que en el fútbol los goles son tan esporádicos que hasta desatan pequeños terremotos en las tribunas. Dividiendo el promedio de 2.6 goles por partido entre los dos equipos que toman parte, esperaríamos que una selección nacional anote 1.3 goles por encuentro, en promedio. Pero si el equipo es superior al promedio, anotará más goles. Por eso hay estadísticos que han calculado la conversión de puntos Elo al valor esperado de goles de un equipo contra otro y la fórmula que proponen es:

Goles por partido = exp (0.2+0.17 (delta/100))

donde “delta” es la diferencia de puntaje Elo entre ambas escuadras. Con este valor esperado, la probabilidad de anotar el número de goles mostrado abajo, contra un contrario con el mismo número de puntos Elo (dos equipos promedio), utilizando la distribución de Poisson, está dada por la Tabla 1.

Tabla 1: Probabilidad de anotar goles con un equipo promedio

Pero si se enfrentan México y Brasil, con una diferencia Elo de 339 puntos, las probabilidades para las respectivas anotaciones de cada equipo son las indicadas en la Tabla 2.

Tabla 2: Probabilidad de anotar el número indicado de goles por Brasil o México

Como se puede ver, es baja la probabilidad de que Brasil se quede sin anotar, pero es de 50% para México. Brasil tiene una probabilidad mayor de anotar dos o tres goles. Claro que un equipo se puede crecer en un partido y lograr el milagro de ganar, especialmente si logra clavar el primer tanto. Curiosamente, en el Mundial de Sudáfrica de 2010, el 92% de las veces ganó el equipo que anotó primero. En la Premier League inglesa el equipo que se adelanta gana el 66% de las veces.

Ya teniendo un modelo de Poisson para cada equipo y encuentro, lo que se hace entonces es simular cada partido de la fase de grupos del Mundial, y de las eliminatorias después de la fase de grupos, para determinar qué equipo es el ganador del torneo. Esto se repite miles de veces y al final solo es cuestión de reportar que tan frecuentemente ganó Brasil, o Argentina, o México, etc. Hay estadísticos que utilizan un modelo de Poisson para el ataque y otro para la defensa, pero esa es una complicación que no vamos a abordar aquí.

Entonces, para simular un juego entre dos selecciones, basta calcular con base en la diferencia de sus rankings Elo y el modelo de Poisson, qué probabilidades tiene cada una de anotar 0, 1, 2 o más goles. Con la computadora se genera un número aleatorio para cada equipo. Es como si tuviéramos un dado para cada escuadra, con siete caras marcadas 0, 1, 2, etc. La probabilidad de que cada cara sea seleccionada por la computadora es la indicada por la tabla de probabilidades. Claro que se trata de un “dado” digital y no material. Existen los métodos apropiados para simular que arrojamos ese dado con las probabilidades correctas.

Tomando la tabla de Brasil/México como referencia, podemos ver que nuestro país anotaría cero goles en el 50% de los partidos, pero 1 o 2 en el 34% y 12% de los partidos, respectivamente. Si simulamos 1000 partidos, por ejemplo, la probabilidad de terminar empatados cero a cero es de 50% multiplicado por 11%, o sea, de solo 5.5%. Claro que hay que hacer notar que el ranking Elo se basa en el pasado reciente, los últimos doce meses, por ejemplo, y un equipo puede crecerse durante el torneo, o bien derrumbarse. Le sucedió a Alemania que no pasó de la fase de grupos en 2018. La simulación es solo un indicador de lo que podría ocurrir durante la Copa del Mundo si todos los equipos se comportan como su ranking indica. Si se lesionan jugadores clave, por ejemplo, el rendimiento puede ser muy distinto.

Simulé la Copa del Mundo de Qatar utilizando un método doble. Para simplificar tomé como punto de partida a los 16 equipos que en las apuestas de deportes son favorecidos para pasar de la fase de grupos. A partir de ahí, y solo para esos 16 equipos, calculé victorias y derrotas utilizando el puntaje Elo. El resultado final es la probabilidad de cada equipo de ganar la Copa del Mundo, suponiendo que se encuentra en el grupo de 16 finalistas y ordenados de acuerdo con los ocho grupos de los que emergen. Las probabilidades que obtengo se muestran en la Tabla 3.

Tabla 3: Simulación de la probabilidad de ganar la Copa del Mundo 2022

El favorito es Brasil, con 26.5% de probabilidad de ganar el Mundial, seguido de Argentina, con 19.9%. México tiene una probabilidad de 0.5% de ganar el torneo, muy cerca de lo que los mercados de apuestas esperan.

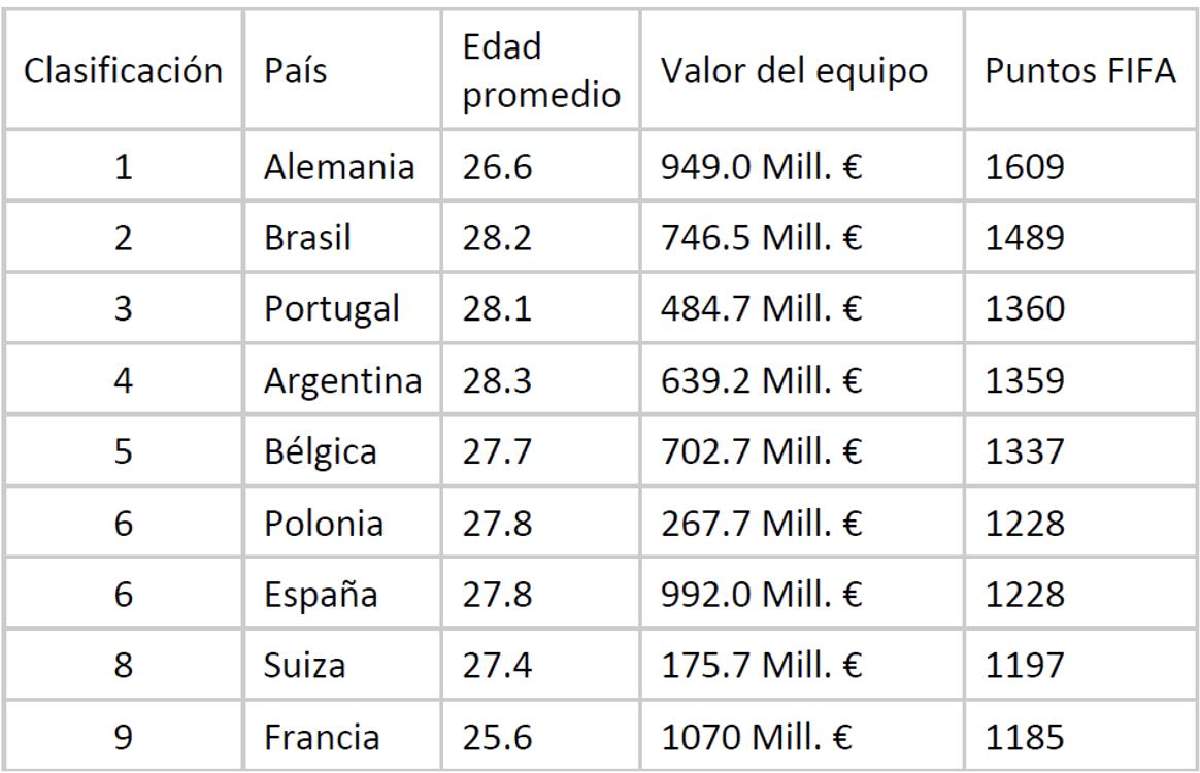
Figura 2. Edad promedio, valor de mercado y puntos FIFA de las 9 mejores seleccione de fútbol, de acuerdo con FIFA (datos de transfermarkt.de y de la FIFA para el mundial de 2018).

Otra posibilidad para tratar de encontrar al ganador es apostar por la selección nacional más cara, de acuerdo con el valor de sus jugadores en el mercado de transferencias. Esto ha funcionado en los últimos mundiales, especialmente en 2018, cuando Francia era la selección más valiosa, y también en 2014 cuando Alemania lo era (Figura 2). Para este año la selección de mayor valor es Inglaterra; Brasil es la segunda más valiosa. Pero ya veremos qué se impone, si la clase brasileña o las libras esterlinas. En los mercados de apuestas a Brasil se le asigna el 20% de probabilidad de ganar la Copa del Mundo, no muy lejos del 26.5% de mi simulación casera. A Inglaterra las apuestas le asignan una probabilidad de 11.8% de ganar el Mundial. Los mercados de apuestas son generalmente un buen indicador de toda la información disponible, aunque los aficionados se dejan llevar muchas veces por sus emociones. En Las Vegas, por ejemplo, las numerosas apuestas por México han duplicado los momios del Tri en solo una semana. Y es que el mejor jugador mexicano es el número 12, la afición.

Referencias

1) R. Rojas, El fútbol bajo el microscopio, Fondo de Cultura Económica, 2022.

https://acmor.org/publicaciones/rese-a-del-libro-el-f-tbol-bajo-el-microscopio

2) D. Adam, “Science and the World Cup: how big data is transforming football”, Nature, 15 Nov 2022.

3) World Football Elo Ratings https://en.wikipedia.org/wiki/World_Football_Elo_Ratings

4) Distribución de Poisson https://es.wikipedia.org/wiki/Distribución_de_Poisson

Esta columna se prepara y edita semana con semana, en conjunto con investigadores morelenses convencidos del valor del conocimiento científico para el desarrollo social y económico de Morelos. Desde la Academia de Ciencias de Morelos externamos nuestra preocupación por el vacío que genera la extinción de la Secretaría de Innovación, Ciencia y Tecnología dentro del ecosistema de innovación estatal que se debilita sin la participación del Gobierno del Estado.