Antonio Gamboa Suárez, Centro de Investigaciones Químicas, Universidad Autónoma del Estado de Morelos
El Dr Antonio Gamboa obtuvo su Doctorado en Fisica por la Universidad Politécnica de Madrid y actualmente es miembro del Centro de Investigaciones Químicas de la Universidad Autónoma del Estado de Morelos.
Esta publicación fue revisada por el comité editorial de la Academia de Ciencias de Morelos.
Leyenda sobre el ajedrez
Cuando pensamos en un fenómeno que presenta causa y efecto, tendemos a creer que el mismo tiene un comportamiento lineal, es decir, que el efecto es proporcional a la causa. Por ejemplo, si estudiamos más tiempo para un examen tendremos una calificación que será proporcionalmente mejor. Si vamos al doble de velocidad, haremos la mitad del tiempo, etcétera. Sin embargo, existen muchísimos fenómenos en la naturaleza que no presentan este comportamiento lineal y deben ser descritos con otro tipo de matemáticas. Para ilustrar el punto, contaré la leyenda de cómo se inventó el ajedrez. Aunque es una historia bastante conocida, sirve para ilustrar perfectamente el tipo de funciones de las que quiero hablar en este artículo.
Se cuenta que había un rey que estaba muy aburrido y entonces decidió convocar a un concurso. A aquel que fuera capaz de inventar un juego que consiguiera divertirlo, le concedería cualquier deseo que le pidiera. Entonces, un hombre del reino inventó el ajedrez y se lo presentó. El rey estaba encantado con la complejidad y posibilidades del juego así que le dijo a su súbdito que podía pedir cualquier deseo. El hombre, como era sabio, decidió darle una lección al rey. Así que le pidió lo siguiente: que tomara un tablero de ajedrez y que en la primera casilla pusiera dos granos de arroz[1]. En la segunda pusiera cuatro, en la tercera ocho y que sucesivamente fuese duplicando la cantidad de granos de arroz hasta llegar a la última casilla, la 64. El rey se rio de la petición y le dijo: -ya que hiciste algo tan bueno, me parece absurdo que me pidas algo tan fácil de cumplir. De cualquier manera, cumpliré tu deseo. Ordenó dar al súbdito la cantidad de arroz que pedía. Sin embargo, al hacer las cuentas con cuidado, los empleados del rey descubrieron que ni siquiera con todo el arroz del reino sería posible cubrir la cantidad de la última casilla, ya que ésta era exorbitante. Con esto, el inventor le dio una nueva lección al rey quien entendió que no podía conceder cualquier cosa por poderoso que fuera.
Haciendo un cálculo no muy exacto, para poder llenar esa última casilla de arroz, se necesitarían alrededor de: ¡1000 veces la cantidad total de arroz que se produce en todo el mundo en un año actualmente! Así que lo que el inventor le estaba enseñando al rey era un ejemplo de un comportamiento exponencial, le estaba mostrando que el pensamiento lineal que el rey solía utilizar para analizar las cosas, no servía en absoluto para describir el reto que le planteó.
Aspectos matemáticos
Tratemos de pensar un poco en el aspecto matemático de este problema. Si vamos agregando cada vez el doble de granos de arroz, conforme vamos avanzando en las casillas, tendremos una secuencia de granos que será la siguiente: 2, 4, 8, 16, 32, 64...Pero esta secuencia se puede escribir también como potencias de 2. Es decir: 21,22,23,24... Si expresamos esto en la forma de una función tendremos la expresión y=2x. Esta expresión, en palabras, dice: si quiero calcular el resultado y (la cantidad de granos de arroz) en la casilla x (donde x puede ser 1, 2, hasta 64), tengo que elevar el número 2 a la potencia x. Estamos entonces ante lo que se conoce como una función exponencial. En una función de este tipo siempre hay 3 componentes. El resultado (y), es decir, la función exponencial en sí misma, el exponente (x), en nuestro caso, las casillas del tablero y la base, que en este caso es el número 2. Este número puede ser diferente y, sin embargo, seguiremos teniendo una función exponencial. Por ejemplo, si el inventor hubiera pedido que se triplicara el número de granos de arroz en cada casilla, la base sería 3 en lugar de 2. Por supuesto, una base más grande hace un crecimiento todavía mayor, pero el comportamiento cualitativo es el mismo, es decir, lo más importante para hablar de este tipo de funciones es el comportamiento exponencial que le da la variable x.
Aparte de esta historia del ajedrez, existen un gran número de fenómenos en la naturaleza que están descritos por un comportamiento exponencial. Algunos ejemplos son: el crecimiento de poblaciones de microorganismos, el interés compuesto y algo que nos ha afectado de manera muy clara en estos últimos dos años: la propagación de una pandemia. Una cuestión importante al analizar un comportamiento exponencial es que, si estamos ya en una zona de alto crecimiento (una casilla avanzada en el tablero de ajedrez), un pequeño movimiento en lo que hagamos (una casilla en el tablero), provocará un cambio enorme en el resultado. Por esta razón es tan extremadamente difícil encontrar estrategias que sean realmente efectivas para controlar este tipo de problemas. Es decir, estamos ante un fenómeno tal que, aunque los epidemiólogos conocen el comportamiento matemático, aun así, es extremadamente complicado de controlar, dada la enorme sensibilidad ante pequeños cambios que tienen estas funciones. Además, es un problema que depende de muchas variables, como las capacidades sanitarias, la situación económica de un país, etcétera. Por tanto, tomar ciertas medidas en algún lugar del mundo, no asegura que funcionará de la misma manera en otro. Tratar de entender un problema como éste, aplicando un pensamiento lineal, como a menudo tienden a hacer algunas personas, es cometer el mismo error que el rey de la historia y al igual que a él, este tipo de razonamiento llevará a resultados completamente erróneos que no contribuirán a resolver un problema tan complejo como éste.
Funciones emparentadas
Existen otras funciones que están emparentadas íntimamente con las exponenciales. En realidad, son sus funciones inversas. Se trata de los logaritmos. Cuando yo los estudié en la secundaria, se empleaban unas tablas para poder calcularlos. Actualmente se usan calculadoras, pero, en la mayoría de los casos, los estudiantes no entienden cuál es la utilidad de estas funciones en la vida cotidiana. Como veremos pronto, se trata de unas funciones que están ligadas a nuestros sentidos y a la forma en que percibimos el mundo.
Si pensamos en el logaritmo como una función, ésta sería, como antes había dicho, la función inversa a la exponencial. Para entender cualitativamente lo que es una función inversa, podemos intercambiar la y y la x en nuestra función exponencial anterior. En este caso, lo que ahora sería la x es el número de granos de arroz y lo que la función y, es decir el logaritmo, daría la casilla a la que corresponde esa cantidad de arroz. También tenemos una base como antes, que en este caso seguiría siendo el mismo número 2. Entonces, sin meternos en más detalles matemáticos, lo que tenemos es un comportamiento inverso. Es decir, ahora tenemos un número que tenemos que ir variando enormemente, mientras que el resultado cambia muy lentamente. En la figura 1, se muestra una representación gráfica de ambas funciones en donde se puede apreciar con mayor precisión lo que queremos decir con comportamiento inverso.

Figura 1: Las funciones exponencial (izquierda) y logarítmica(derecha) con base 2.
Existe una ley publicada por primera vez en 1860 que se conoce como ley de Weber-Fechner. Es una ley que habla de la percepción y establece una relación entre la magnitud de un estímulo y la forma en que éste es percibido por los sentidos. Pues bien, resulta que ésta es una ley logarítmica. Es decir, la magnitud del estímulo debe ir siendo mayor en una proporción exponencial, para que nosotros percibamos un cambio de manera lineal. Tenemos unos sentidos que interactúan con la realidad de manera logarítmica. Existen una gran cantidad de ejemplos que abarcan prácticamente la totalidad de nuestros sentidos. Un ejemplo lumínico sería el siguiente. Supongamos que tenemos una vela encendida, al encender una segunda vela, percibiremos un cambio en la luminosidad de la habitación. Ahora hay dos velas prendidas. Para sentir un cambio equivalente, necesitaremos prender dos velas más, después cuatro, etcétera. Es decir, tendremos una percepción logarítmica de la luminosidad de la habitación. El número de velas debe crecer como los granos de arroz y nuestra percepción lo hará como las casillas del tablero. Otra característica importante es que el umbral para que el cambio en el estímulo sea perceptible, depende del tamaño del estímulo en si mismo. Mientras más grande sea éste, mayor tiene que ser el cambio para que percibamos un cambio (1). Veamos algunos ejemplos más que afectan a otros de nuestros sentidos.
En la música, la percepción de un tono más agudo o más grave depende de la frecuencia de la onda sonora que se emite. Esto se ilustra en la figura 2. Por convención, la frecuencia de la nota "La" que se encuentra en el centro de un piano es de 440 Hz (2). Dada la secuencia Do, Re, Mi, Fa, Sol, La, Si, Do; al llegar nuevamente a la misma nota de la que partimos, tenemos lo que se llama una octava. Pues bien, al llegar a la siguiente "La" a la derecha del piano, la frecuencia es ahora de 880 Hz, es decir, se ha duplicado. Y así sucesivamente irá sucediendo a cada octava que nos movamos. Justamente de la misma manera que los granos de arroz en el tablero. Sin embargo, nuestra percepción de los agudos será que la nota se ha vuelto más aguda, en la misma proporción para cada octava. Es decir, percibimos lo agudo de las notas de manera logarítmica. Igualmente tenemos otro parámetro que en este caso mide no el tono sino la intensidad de la onda sonora. La unidad que mide la relación entre dos potencias sonoras se conoce como decibelio. Nuevamente, nuestra percepción de la intensidad de una onda sonora será también logarítmica, solo que en este caso es aún más drástico dado que la base es 10 y no 2. Es decir, los cambios en el estímulo van en potencias de 10: 10, 100, 1000, etcétera (3).
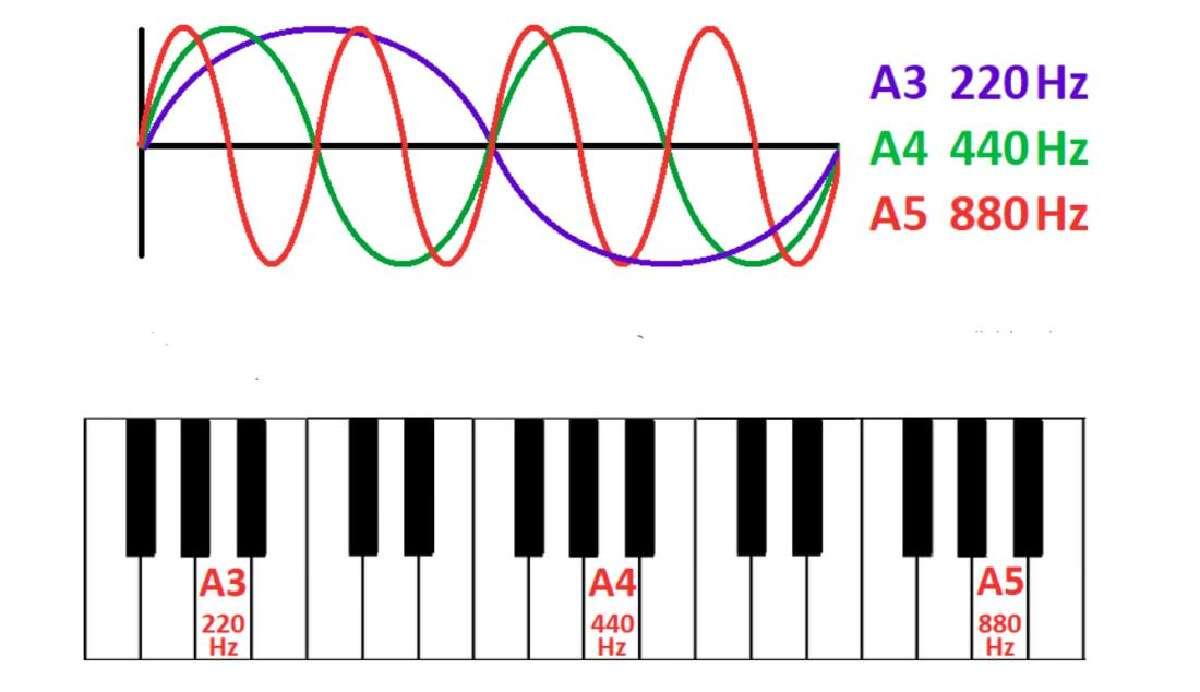
Figura 2: Diferentes octavas en el piano. Tomado de https://miguitarraelectrica.com/frecuencias-sonidos-armonicos/
Termino con dos ejemplos de cosas muy diferentes, pero con las cuales estamos muy familiarizados en México. Una de las escalas utilizadas para evaluar y comparar la intensidad de los sismos, se conoce como escala de Richter (ver figura 3), desarrollada por los sismólogos Charles Richter y Beno Gutemberg (4) en 1935. Nuevamente se trata de una escala logarítmica relacionada con la amplitud (intensidad) de la onda sísmica. Así que nuevamente, si tenemos dos sismos de la misma duración, pero el primero de una intensidad 10 veces mayor que el otro, nos producirá la sensación de un cambio de un grado en la escala. Por esta razón, la diferencia en cuanto a poder devastador de un sismo de, pongamos 6 grados a uno de 7 es enorme, aunque por supuesto se trata de un fenómeno mucho más complicado y hay que tomar en cuenta una gran cantidad de factores adicionales para hacer una evaluación adecuada en ese sentido.

Figura 3: Escala de Richter. Tomada de https://sites.ipleiria.pt/seismicknowledge/tag/escala-de-richter/
El último ejemplo afecta a nuestro sentido del gusto. A muchos mexicanos nos encantan las cosas picantes. La sustancia que le confiere el picor a los chiles se conoce como capsaicina. Una de las escalas más utilizadas para medir el picor de un chile, se le conoce como escala Scoville, desarrollada por Wilbur Scoville en 1912 (5). La escala es un tanto subjetiva, ya que consiste en partir de una cierta solución de extracto de chile y realizar diluciones sucesivas de la misma en agua con azúcar hasta que un grupo de expertos no sean capaces de detectar la más mínima presencia de picante. El número de diluciones que es necesario hacer, da la escala Scoville del chile en particular. Una vez más, nos encontramos en un proceso, donde la cantidad de chile va disminuyendo de manera exponencial, por tanto, es un caso más de percepción logarítmica (figura 4).

Figura 4. Escala Scoville. Tomado de https://www.agromatica.es/scoville/
Vivimos en un universo extremadamente diverso y rico en fenómenos de todo tipo. Las matemáticas son el lenguaje que hemos encontrado que mejor logra describir el comportamiento de la naturaleza. Y para describir adecuadamente el comportamiento de muchos fenómenos interesantes, es necesario ir más allá del comportamiento lineal y encontrar funciones que describan adecuadamente lo que observamos. Una de estas funciones es el caso de los logaritmos, los cuales sirven para describir matemáticamente la forma en que nuestros sentidos perciben el mundo que les rodea.
Esta columna se prepara y edita semana con semana, en conjunto con investigadores morelenses convencidos del valor del conocimiento científico para el desarrollo social y económico de Morelos. Desde la Academia de Ciencias de Morelos externamos nuestra preocupación por el vacío que genera la extinción de la Secretaría de Innovación, Ciencia y Tecnología dentro del ecosistema de innovación estatal que se debilita sin la participación del Gobierno del Estado.
Referencias
(1) http://optimaticosum.blogspot.com/2013/09/los-logaritmos-y-la-percepcion.html
(2) https://miguitarraelectrica.com/frecuencias-sonidos-armonicos/
(3) http://hyperphysics.phy-astr.gsu.edu/hbasees/Sound/db.html
(4) https://sites.ipleiria.pt/seismicknowledge/tag/escala-de-richter/
(5) https://www.agromatica.es/scoville/





