Un estimado colega está siempre a la caza de historias científicas interesantes. En esta ocasión nuestro buen amigo nos comparte el presente artículo, publicado en el boletín digital Sicence Daily con información provista originalmente por la University of Kent (UK) en Inglaterra el pasado 31 de agosto de 2021 y traducido por nosotros, en el que nos informan que investigadores de esa universidad descubrieron una fórmula matemática universal que puede describir el huevo de cualquier pájaro, reptil o pez existente en la naturaleza, un paso significativo en la comprensión no solo de la forma del huevo en sí, sino también de cómo y por qué evolucionó, lo que posibilita aplicaciones biológicas y tecnológicas generalizadas. Veamos de qué se trata….

La forma de huevo ha atraído durante mucho tiempo la atención de matemáticos, ingenieros y biólogos desde un punto de vista analítico. La forma ha sido muy apreciada por su evolución, ya que es lo suficientemente grande como para incubar un embrión, lo suficientemente pequeño para salir del cuerpo de la manera más eficiente, no rodar una vez puesto, es estructuralmente lo suficientemente sólida como para soportar peso y ser el inicio de la vida por tanto de muchas especies. Al huevo se le ha llamado la "forma perfecta".
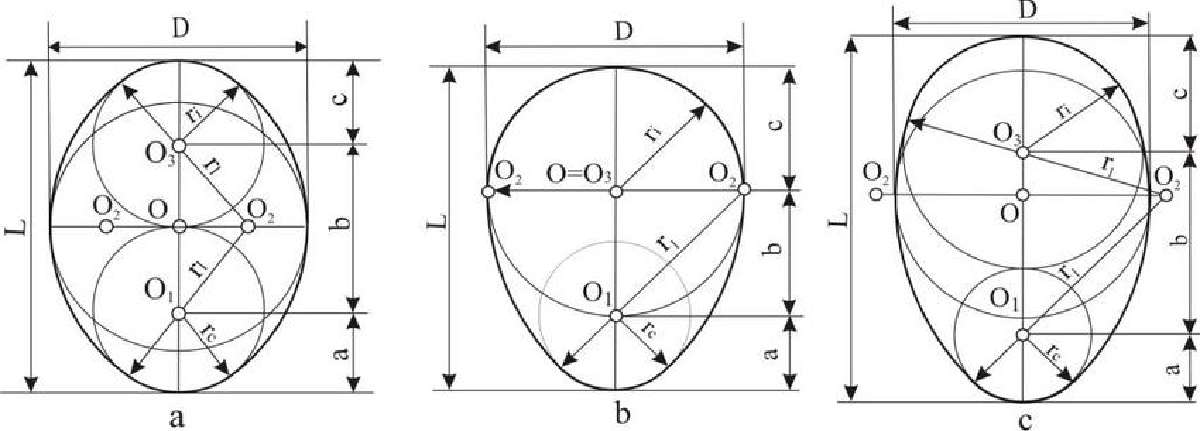
El análisis de todas las formas de huevo utilizó cuatro figuras geométricas: esfera, elipsoide, ovoide y piriforme (cónica o en forma de pera), con una fórmula matemática para la piriforme que aún no se ha derivado.
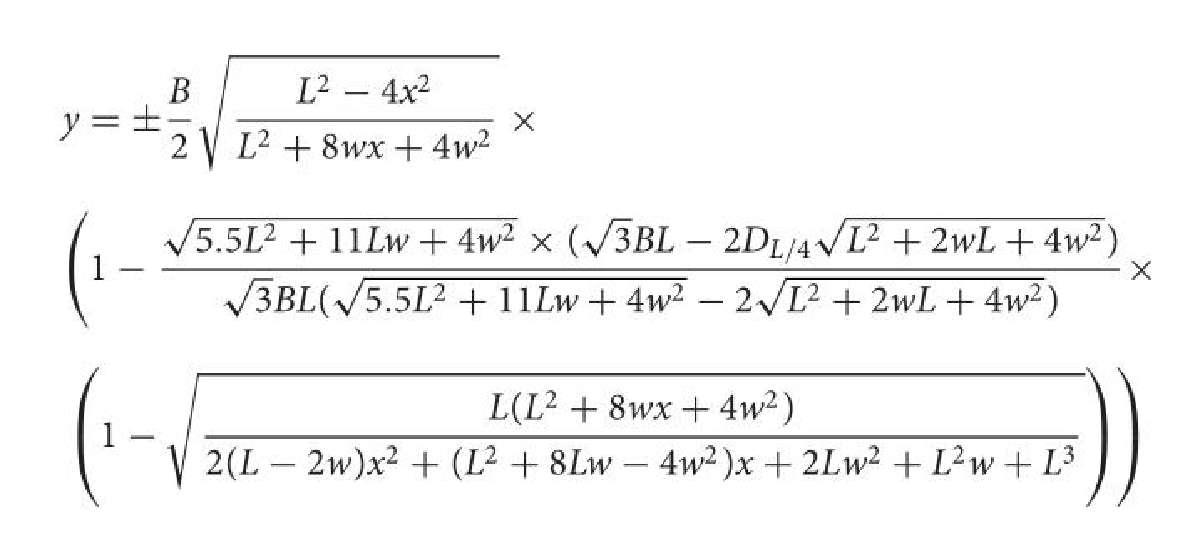
Para rectificar esto, los investigadores introdujeron una función adicional en la fórmula ovoide, desarrollando un modelo matemático para adaptarse a una forma geométrica completamente novedosa caracterizada como la última etapa en la evolución de la esfera-elipsoide, que es aplicable a cualquier geometría de huevo.
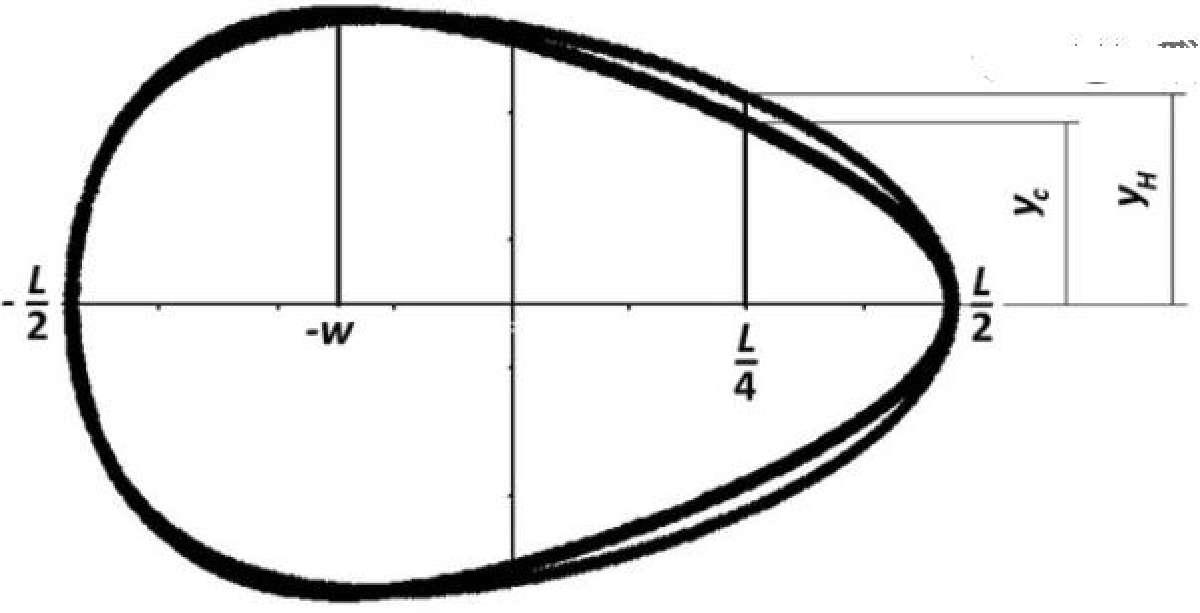
Esta nueva fórmula matemática universal para la forma del huevo se basa en cuatro parámetros: longitud del huevo, anchura máxima, desplazamiento del eje vertical y diámetro a un cuarto de la longitud del huevo.
Esta fórmula universal tan buscada es un paso significativo en la comprensión no sólo de la forma del huevo en sí, sino también de cómo y por qué evolucionó, lo que hace posibles aplicaciones biológicas y tecnológicas generalizadas.

Las descripciones matemáticas de todas las formas básicas de huevos ya han encontrado aplicaciones en la investigación alimentaria, la ingeniería mecánica, la agricultura, las biociencias, la arquitectura y la aeronáutica. Como ejemplo, esta fórmula se puede aplicar a la construcción de ingeniería de recipientes de paredes delgadas con forma de huevo, que deberían ser más fuertes que los típicos esféricos.
Esta nueva fórmula es un avance importante con múltiples aplicaciones que incluyen:

- Descripción científica competente de un objeto biológico. Ahora que un huevo puede describirse mediante una fórmula matemática, el trabajo en los campos de la sistemática biológica, la optimización de los parámetros tecnológicos, la incubación del huevo y la selección de las aves de corral se simplificarán enormemente.

- Determinación precisa y sencilla de las características físicas de un objeto biológico. Las propiedades externas de un huevo son vitales para los investigadores e ingenieros que desarrollan tecnologías para incubar, procesar, almacenar y clasificar huevos. Existe la necesidad de un proceso de identificación simple que utilice el volumen del huevo, el área de la superficie, el radio de curvatura y otros indicadores para describir los contornos del huevo, que proporciona esta fórmula.

- Ingeniería inspirada en la biología del futuro. El huevo es un sistema biológico natural estudiado para diseñar sistemas de ingeniería y tecnologías de vanguardia. La figura geométrica en forma de huevo se adopta en la arquitectura, como el techo del Ayuntamiento de Londres y el pepinillo, y la construcción ya que puede soportar cargas máximas con un consumo mínimo de materiales, a los que ahora se puede aplicar fácilmente esta fórmula.

Darren Griffin, profesor de genética en la Universidad de Kent e investigador principal de la investigación, dijo: "Los procesos evolutivos biológicos como la formación de huevos deben investigarse para la descripción matemática como base para la investigación en biología evolutiva, como se demuestra con esta fórmula. La fórmula se puede aplicar en disciplinas fundamentales, especialmente en la industria alimentaria y avícola, y servirá de impulso para futuras investigaciones inspiradas en el huevo como objeto de investigación ".

El Dr. Michael Romanov, investigador visitante de la Universidad de Kent, dijo: "Esta ecuación matemática subraya nuestra comprensión y apreciación de una cierta armonía filosófica entre las matemáticas y la biología, y de esas dos un camino hacia una mayor comprensión de nuestro universo, entendido claramente en la forma de huevo ".

El Dr. Valeriy Narushin, ex investigador visitante de la Universidad de Kent, dijo: "Esperamos ver la aplicación de esta fórmula en todas las industrias, desde el arte hasta la tecnología, la arquitectura y la agricultura. Este avance revela por qué la investigación colaborativa de disciplinas separadas es esencial".

El documento "Huevo y matemáticas: introducción de una fórmula universal para la forma del huevo" se publica en Anales de la Academia de Ciencias de Nueva York (Valeriy G. Narushin, Instituto de Investigación para el Tratamiento Ambiental y Vita-Market Ltd, Ucrania; Dr. Michael N. Romanov , Universidad de Kent; Profesor Darren K. Griffin, Universidad de Kent).
Fuentes: https://www.sciencedaily.com/releases/2021/08/210827133748.htm n




