Gabriela Hinojosa obtuvo el grado de Doctora en Ciencias en el Instituto de Matemáticas de la UNAM, en 2002. Desde el 2003 es Profesora Investigadora de Tiempo Completo adscrita al Centro de Investigación en Ciencias de la Universidad Autónoma del Estado de Morelos (UAEM). Es integrante del Sistema Nacional de Investigadores y posee la distinción perfil PRODEP. Es miembro de la Academia de Ciencias de Morelos, directora del Centro de Investigación en Ciencias y Presidenta del Consejo Directivo del Instituto de Investigación en Ciencias Básicas y Aplicadas de la UAEM.
Esta publicación fue revisada por el comité editorial de la Academia de Ciencias de Morelos.
Los nudos forman parte de nuestra vida diaria, los empleamos cuando amarramos las agujetas de nuestros zapatos, o amarramos algún cordón, cuerda, o liga, etc. En este sentido, podemos inferir que los nudos fueron creados para ayudar al ser humano a cubrir algunas de sus necesidades. Desde el punto de vista de las matemáticas, pensamos en un nudo como un pedazo de cuerda en el que se unen sus dos extremos. Por ejemplo, consideremos una cuerda y realicemos el nudo más sencillo (Fig. 1)
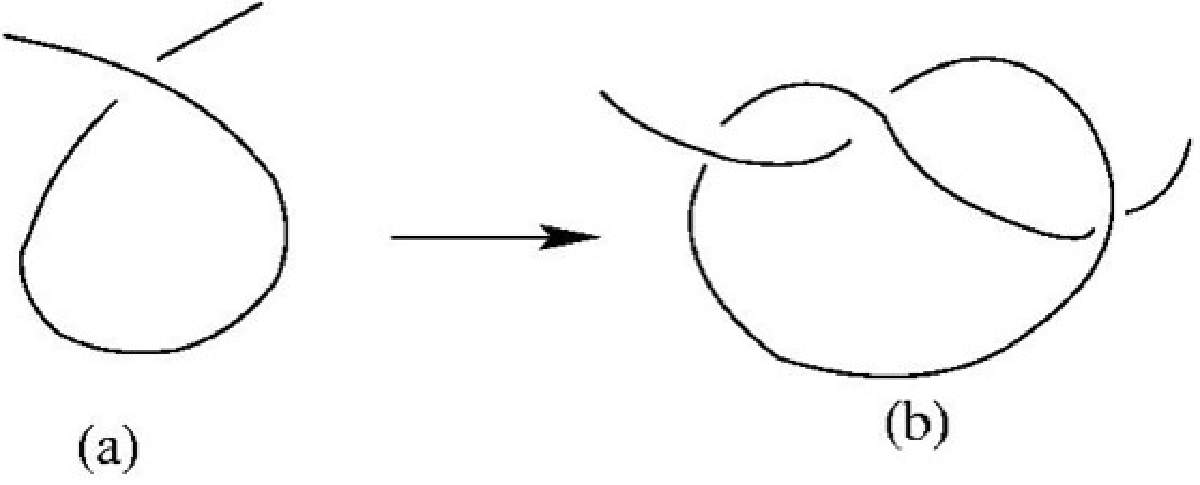
Figura 1. Un nudo sencillo.
Si pegamos los extremos de la cuerda en (b) obtenemos lo que en matemáticas conocemos como el nudo trébol (lado izquierdo de la Fig. 2).
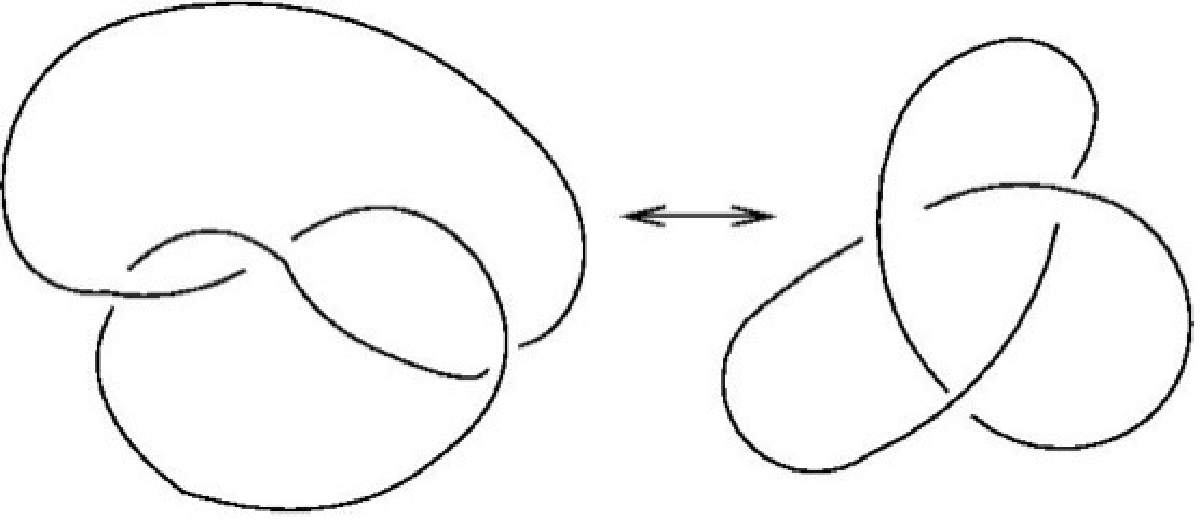
Figura 2. El nudo trébol.
Lo que observamos en la Fig. 2 se les denomina diagrama del nudo y como podemos notar, el diagrama del lado derecho muestra tres cruces que representamos con una lína continua al segmento que “pasa por arriba” y una línea cortada al que “pasa por abajo” ([1]). Ambos diagramas representan al mismo nudo, debido a que podemos transformar el diagrama izquierdo en el derecho si desplazamos los segmentos de la cuerda, sin cortar, alargando los que conforman a los dos óvalos localizados entre dos cruces consecutivos, en matemáticas lo denominamos equivalencia topológica. La topología es la rama de las matemáticas que estudia las propiedades de los objetos geométricos que permanecen invariantes bajo transformaciones continuas; grosso modo, podemos estirar, acortar, o simplemente deformar nuestro objeto, pero no podemos romperlo o cortarlo.
Antecedentes
El origen de los nudos es difícil de establecer, ya que desde la antigüedad se han utilizado de diversas formas, por ejemplo, en la caza, en la pesca, en la vestimenta, en la construcción, etc. Los nudos más antiguos que se conocen datan de 18,500 años y se localizan en vestigios situados en Monte Verde, Chile. Además se han encontrado nudos en Dinamarca con 10,000 años de antiguedad, Finlandia con 7,000 años de antigüedad, etc. Por tal motivo, podemos decir que los nudos nacieron con la civilización humana y su comprensión ha ido avanzando junto al desarrollo de ésta.
En América, los incas desarrollaron un sistema de numeración decimal posicional mediante el uso de un conjunto de cuerdas colgantes con nudos denominado quipus. Los quipus tenían un mínimo de tres cuerdas y un máximo de 2000 para representar números. Un quipu consiste de un conjunto de cuerdas con cierta disposición, en las que se hacen una serie de nudos, en cada cuerda se representaba un número mediante conjuntos de nudos, tal que cada conjunto correspondía a una potencia de diez. La primera información que se dispone al respecto proviene de la obra “Nueva crónica y buen gobierno” escrita por Felipe Guaman Poma de Ayala al rey de España, misma que contiene varios dibujos de quipus [3].
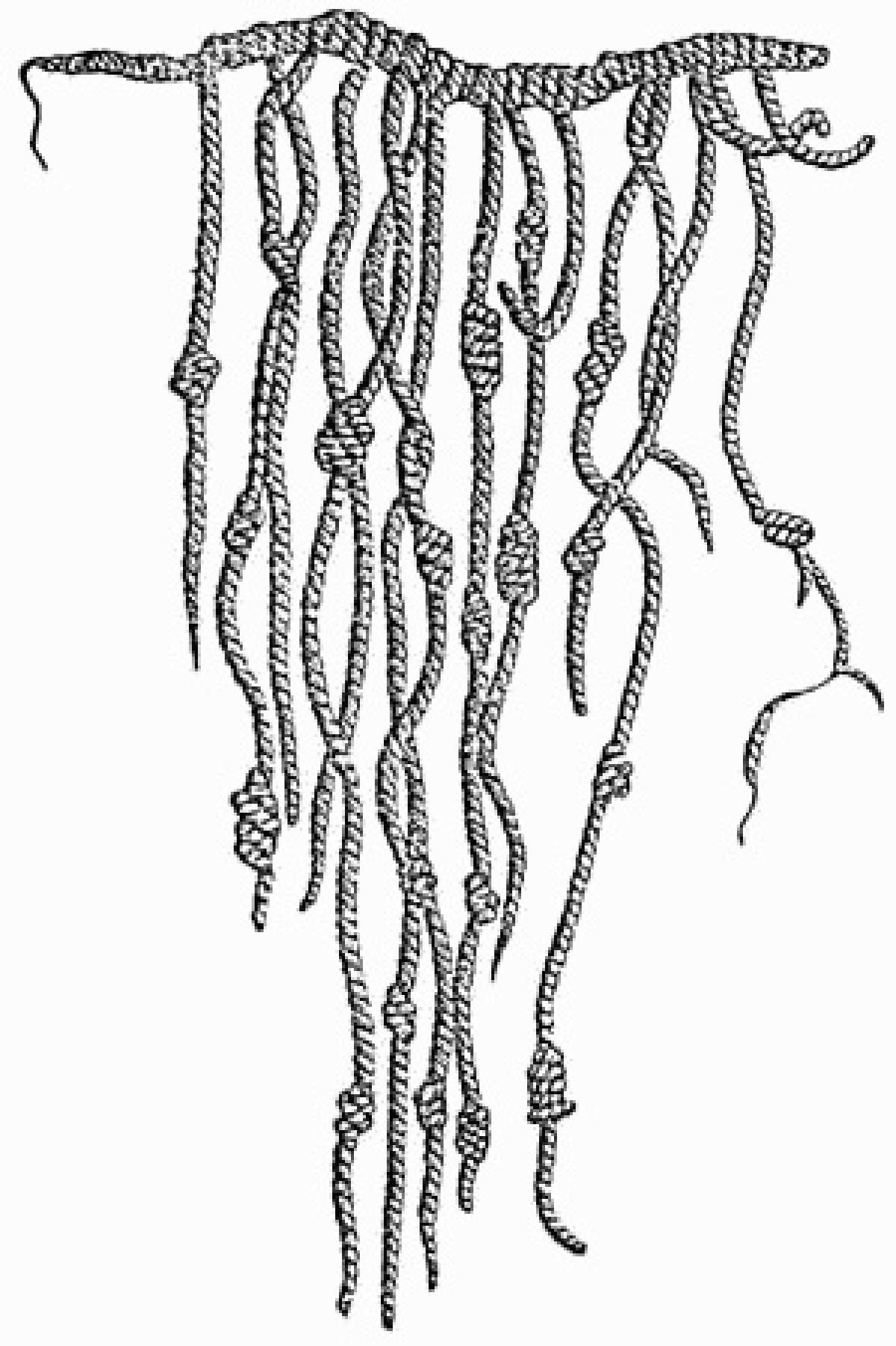
Figura 3. Imagen de un quipu. (Esta imagen ha sido extraída del archivo, Dominio público, https://commons.wikimedia.org/w/index.php?curid=123557)
Los nudos también han sido usados por algunas culturas antigüas como símbolos místicos por su misteriosa belleza, un ejemplo de ello es la cultura Celta, donde los nudos no solo se utilizaban con fines decorativos, ellos iban más lejos y los empleaban para representar el amor, lo eterno tanto de la naturaleza como del alma, el ciclo infinito de la vida, etc. En el arte decorativo celta, se pueden identificar ocho nudos elementales que forman una base para casi todos los patrones. Este sería uno de los primeros pasos hacia una abstracción, debido a que algunas representaciones conducen a problemas geométricos.

Figura 4. Del lado izquierdo, la Cruz Celta (Imagen de De Tracy de North Brookfield, Massachusetts, USA - Flickr, CC BY 2.0, https://commons.wikimedia.org/w/index.php?curid=1694210). Del lado derecho, varios nudos celtas (Esta imagen ha sido extraida de https://www.shutterstock.com/es/search/nudo-celta).
Como mencionamos anteriormente, un importante ejemplo del uso de los nudos es en la navegación marítima; los marineros creaban nudos distintos apropiados cada necesidad, y los transmitían a las siguientes generaciones por medios orales. Notamos la reelevancia de distinguir los diversos nudos en la práctica.
Los marineros no eran los únicos creadores de nudos. Podemos mencionar otros para los que son indispensables incluso hoy en día, como los pescadores, alpinistas y tejedores. Un uso más reciente se observa en espectáculos brindados por magos, donde realizan escapes asombrosos de ataduras que se deshacen misteriosamente; ésto debido a que dichas ataduras son nudos equivalentes a un círculo o trozo de cuerda no anudado. Vemos de nuevo la importancia de distinguir entre diversas clases de nudos en términos prácticos, importancia que la ciencia tardó algunos cientos de años en precisar.
Algunos historiadores sitúan el nacimiento de la teoría de nudos en el siglo XVIII, con un artículo de A.T. Vandermonde (1735-1796), en el cual describe la importancia de cómo está colocado un objeto en el espacio y no de sus medidas. Sin embargo, se puede considerar que el primero en estudiar los nudos como objetos matemáticos fue Carl Friedrich Gauss (1777-1855), en su obra "A Collection of Knots", donde mostró 13 bocetos de nudos con sus respectivos nombres.
En 1834, Johann Benedict Listing (1806-1882), alumno de Gauss, consideró por primera vez a los nudos como círculos anudados, lo cual constituye el nacimiento del concepto matemático de nudo. Listing además introdujó la asociación de diagramas a los nudos, simbolizando los cruces.
Un problema central en matemáticas es clasificar objetos matemáticos de acuerdo a sus diferencias esenciales, ignorando diferencias irrelevantes, es decir, dar una lista de clases de objetos; en nuestro caso es dar una lista de nudos diferentes. El matemático escocés Peter Tait (1831-1901) dedicó gran parte de su trabajo a este problema al que denominó el problema del censo. Su objetivo era encontrar y enumerar todos los posibles nudos que se pueden representar mediante diagramas planos con un número determinado de cruces. Tait también introdujo el concepto de grado de nudo, que se refiere al número mínimo de cruces necesarios para representar al nudo.
Teoría de Nudos
Un “nudo matemático” o simplemente un “nudo” es, para nuestros fines, una curva cerrada simple (que no se auto intersecta) en el espacio (Fig. 5).
Figura 5. El nudo trivial.
Existen muchos nudos, como los mostrados en la Fig. 6:
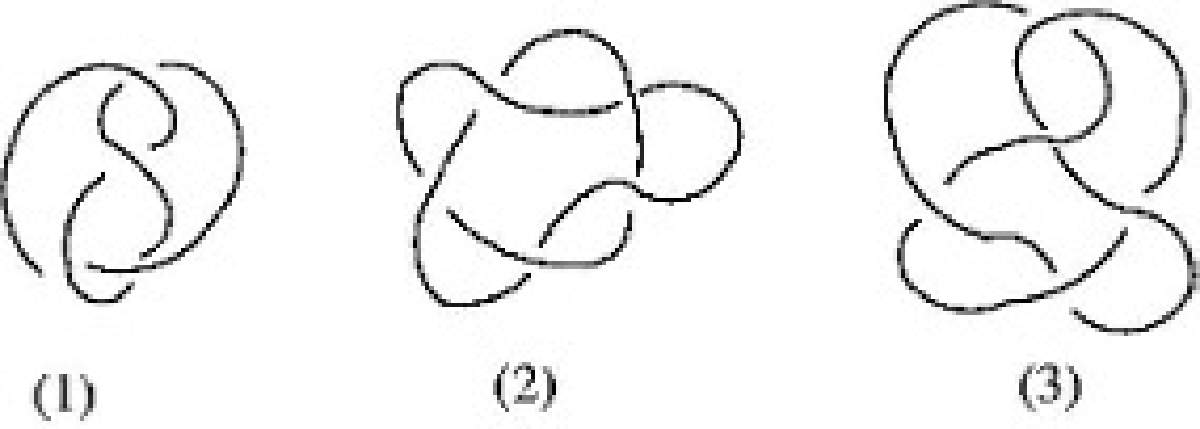
Figura 6. Tres nudos
Consideremos los nudos (1) y (2) en la Fig. 6. A simple vista lucen diferentes, pero ¿existirá la manera de cambiar el nudo (1) en el nudo (2)? Es decir, ¿podemos manipular la forma del nudo (1), cambiándolo lentamente (estirándolo, reduciéndolo) y sin cortarlo, para obtener la forma del nudo (2)? Si esto es posible, decimos que los nudos son equivalentes.
En general, poder decidir si dos nudos son equivalentes es sumamente difícil, por ejemplo considere los nudos mostrados en la Fig. 7,

Figura 7. Nudos equivalentes
Estos nudos, a pesar de que a simple vista parecen completamente distintos, son equivalentes (Fig. 7).
Para abordar este problema, nos enfocaremos en lo que conocemos como nudos mansos, es decir nudos equivalentes a nudos poligonales. Un nudo poligonal es una curva cerrada simple en el espacio que consiste en la unión de un número finito de segmentos rectilíneos que no se autointersecta. En la Fig. 8, el nudo trébol del lado derecho es poligonal, mientras que el del lado izquierdo es lo que denominamos un nudo “suave”.
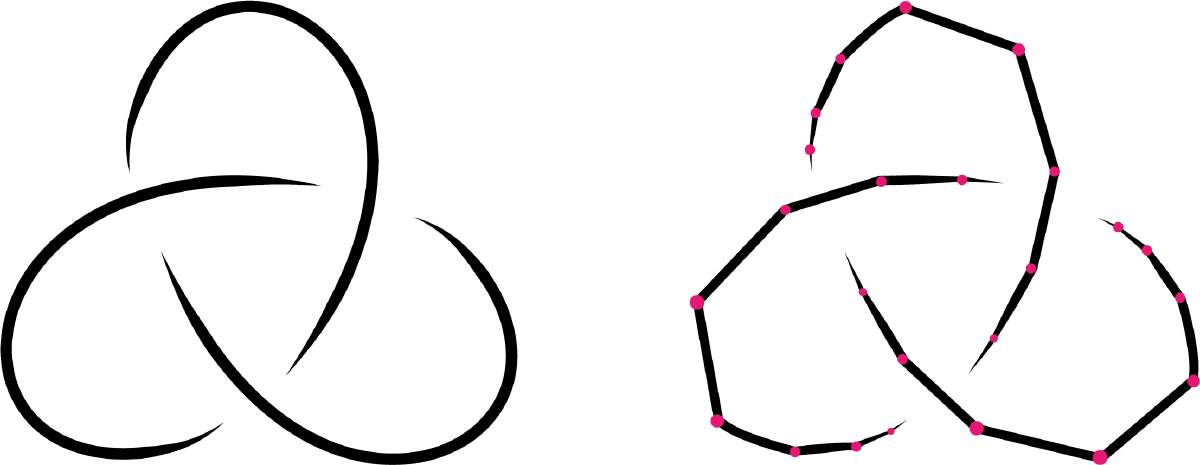
Figura 8. Nudos suaves y nudos poligonales.
Ahora introducimos el concepto de diagrama de un nudo que es una proyección ortogonal del nudo a un plano tal que existe una cantidad finita de puntos de intersección o cruces que provienen de dos puntos distintos del nudo, cuyas proyecciones coindicen, se representan por un segmento que “está encima” y el otro segmento que “está abajo” se marca con una interrupción (Fig. 8). De aquí surge una pregunta fundamental ¿cuándo dos diagramas representan al mismo nudo?
En 1926, el matemático germano Kurt Reidemeister (1893-1971) probó que si tenemos dos diagramas distintos del mismo nudo, entonces podemos ir de un diagrama al otro via una serie de movimientos de Reidemeister. Estos movimientos son de tres tipos (Fig. 9)
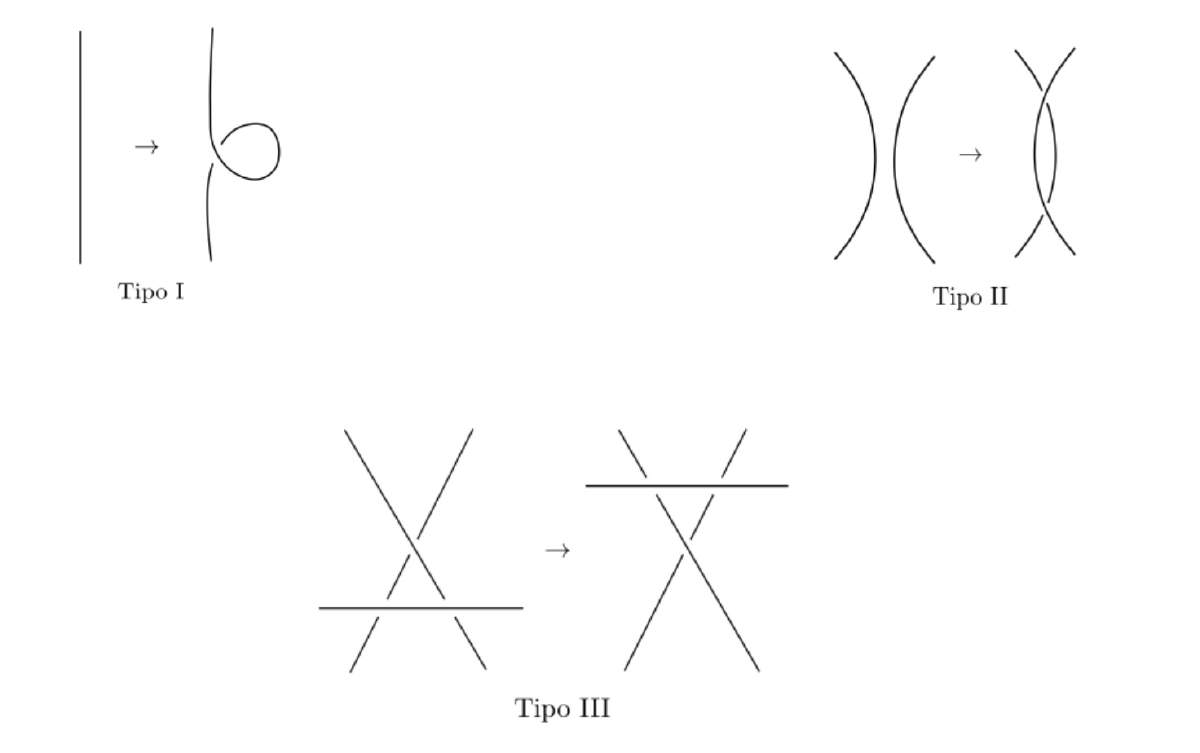
Figura 9. Movimientos de Reidemeister
Además, probó que dos nudos son equivalentes si y sólo si sus respectivos diagramas son equivalentes ([1]). Aparentemente, Reidemeister resuelve el problema, sin embargo no proporciona un algoritmo para determinar si dos nudos son equivalentes, dicho de otra manera, no establece el número de movimientos requeridos para transformar un diagrama en otro.
Para poder distinguir nudos, en 1929 se introduce la noción de invariantes ([5]). Un invariante de nudos es una función que a cada nudo le asocia una estructura algebraica, que puede ser un número, un polinomio, etc., de tal forma que si estas estructuras algebraicas no son equivalentes, entonces los nudos son distintos; sin embargo, si las estructuras son iguales, no podemos deducir si los nudos son equivalentes o no, por lo que los invariantes nos brindan mucha información, pero siguen siendo insuficientes para distinguirlos en todos los casos. Algunos ejemplos de invariantes son: número mínimo de cruces, tricoloreabilidad, el grupo de un nudo, el polinomio de Alexander, el polinomoio de Jones, el polinomio de Kauffman, etc.
Una colección finita de nudos {K1, K2, . . . , Kn} que no se intersectan entre sí, se le llama enlace, tal que cada nudo Ki es una componente del enlace. Al igual que en nudos, tenemos la noción de equivalencia de enlaces. Decimos que dos enlaces L1={K1, K2, . . . , Kn} y L2={K1´, K2´, . . . , Km´} son equivalentes si tienen el mismo número de componentes, es decir, si n=m y si podemos cambiar K1 en K1´, K2 en K2´, y así sucesivamente hasta cambiar Kn en Km´; sin intersectar ninguna otra componente y sin cortar (para más detalles se puede consultar [1]).
Una aplicación al estudio del ADN
Los seres vivos (una persona, animal, planta, etc) está compuesto por moléculas y dentro de cada una de ellas podemos encontrar el ADN. F. H. C. Crick y J. D. Watson describieron la estructura básica del ADN, por lo cual recibieron el premio Nobel de medicina en 1962. En general, la estructura de una molécula de DNA consiste en dos cuerdas entrelazadas en forma de una doble hélice con un eje lineal. En ocasiones se ha encontrado que el ADN tiene la forma de un anillo formado por una o dos cuerdas enrolladas en una doble hélice ([4]).
Para facilitar el estudio de la molécula del ADN dentro de una célula, lo simplificaremos como un hilo en forma de segmento o círculo, y debido a que es muchísimo más largo que el diámetro del núcleo de la célula donde se encuentra, debe estar enredada. Más aún, una pieza de DNA puede romperse temporalmente y durante este estado de rompimiento, su estructura puede someterse a un cambio físico, para posteriormente reunirse. De hecho, a inicios de la década de 1970, se descubrió que unas enzimas llamadas topoisomerasas facilitaban dicho proceso.
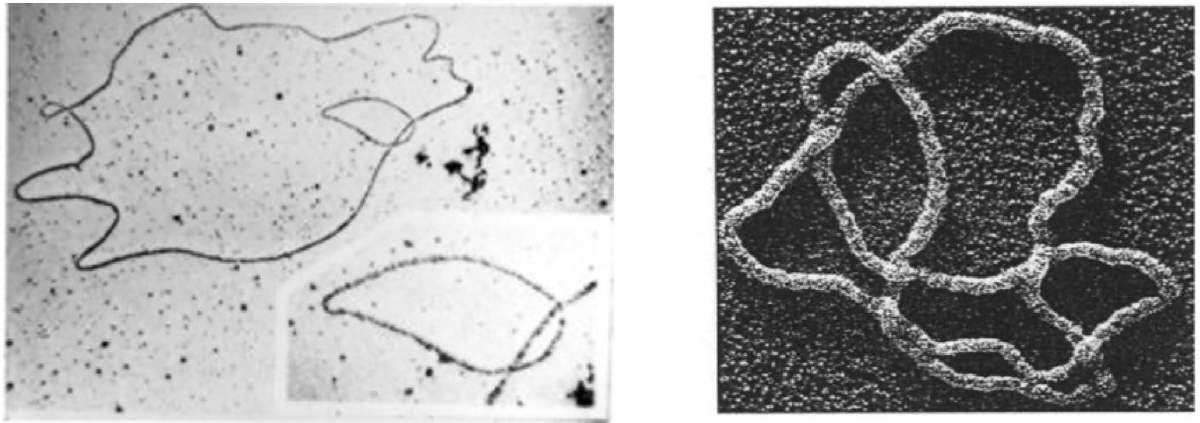
Figura 10. Imagen de microscopía electrónica que muestra la molécula de DNA dentro del núcleo de una célula ( Sumners, D. 1995. Lifting the curtain: Using topology to probe the hidden action of enzymes. Notices of the AMS 42:528-537).
La manera en que una molécula de ADN se enreda, se tuerce (gira sobre su eje) y, por qué no, se anuda, interfiere directamente con los procesos vitales de replicación, transcripción y recombinación del ADN. A su vez al realizar estos procesos, las enzimas (topoisomerasas) manipulan al ADN cambiando la forma en que éste está colocado dentro de la molécula. Por ejemplo, una molécula tiene forma de un círculo sin anudar se puede convertir en un nudo trébol.
El término topoisomerasa puede parecer extraño, sin embargo, proviene de lo siguiente. Químicamente, dos moléculas con la misma composición química pero diferente estructura son llamadas isómeros. Se sigue que dos moléculas de ADN con la misma secuencia de parejas base, pero diferentes números de enlace son también llamadas isómeras. El número de enlace se obtiene sumando las intersecciones de una de las hebras de ADN con la superficie virtual que genera la otra. Debido a la diferencia en los números de enlace, topológicamente no son equivalentes, y estas moléculas de ADN son llamadas topoisómeros. De aquí que la enzima que causa que el número de enlace cambie es llamada topoisomerasa.
El proceso de cambio en una molécula de ADN debido a una topoisomerasa se puede describir grosso modo, de la siguiente manera: una cuerda del ADN es cortada en algún lugar, entonces un segmento de ADN pasa a través de este corte, y finalmente el ADN se reconecta a sí mismo. En el caso más simple, esto es logrado por una topoisomerasa. Sin embargo, también pueden participar sistemas de recombinación sitio-específico, causando un cambio mayor en la molécula.
Un ejemplo de lo anterior, es lo siguiente: Se reconocen los sitios de recombinación, que son dos fragmentos lineales de ADN dentro de la misma molécula (Fig. 11). Esta es una enzima cuyos sitios de recombinación tienen la misma orientación global (hay enzimas cuyos sitios de recombinación tienen orientaciones opuestas).
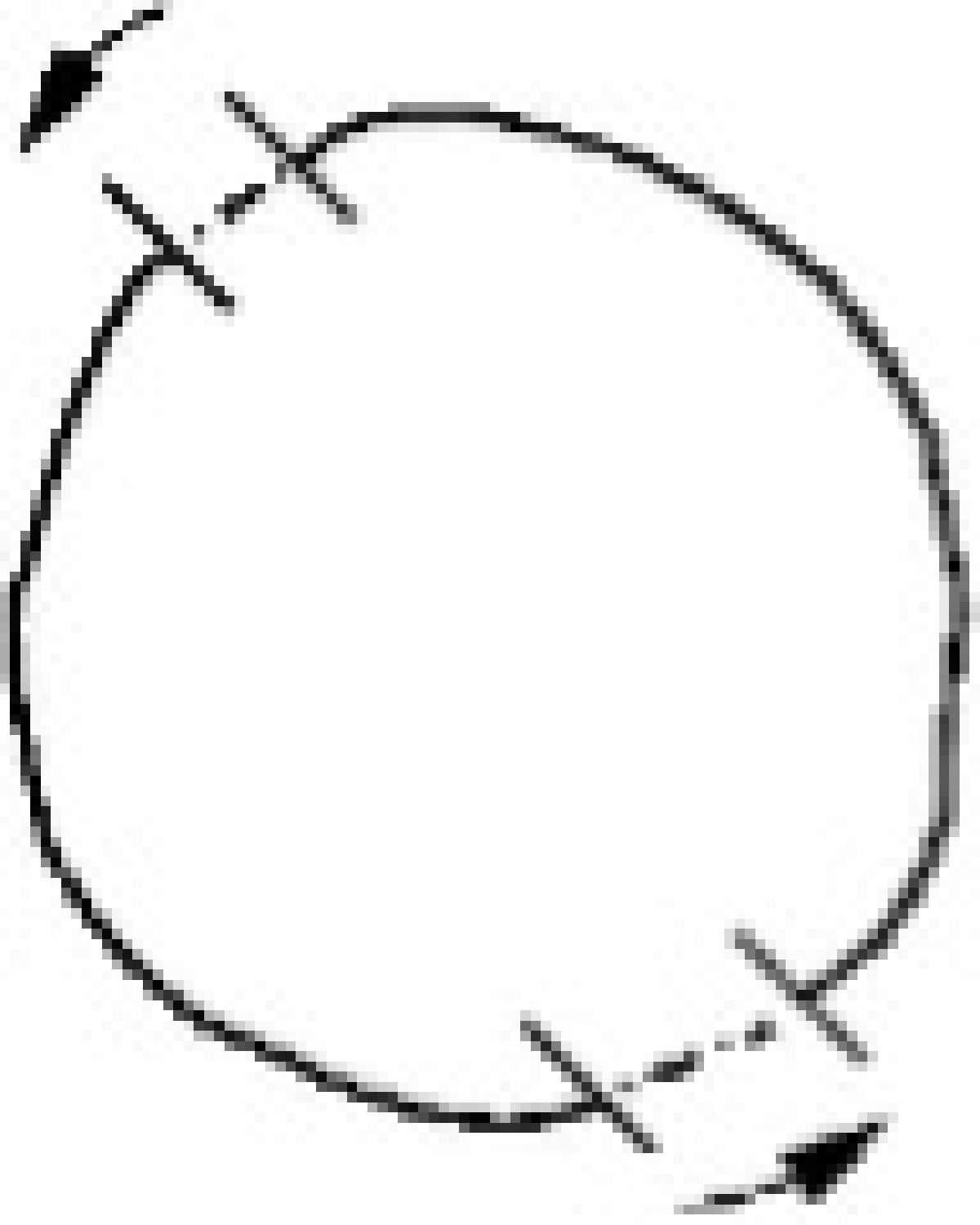
Figura 11. Una molécula de ADN con dos sitios de recombinación en orientación directa.
Se mueve la molécula de manera que los sitios quedan uno frente al otro. Aquí llega la enzima y corta las cadenas para volver a pegar (Fig. 12)
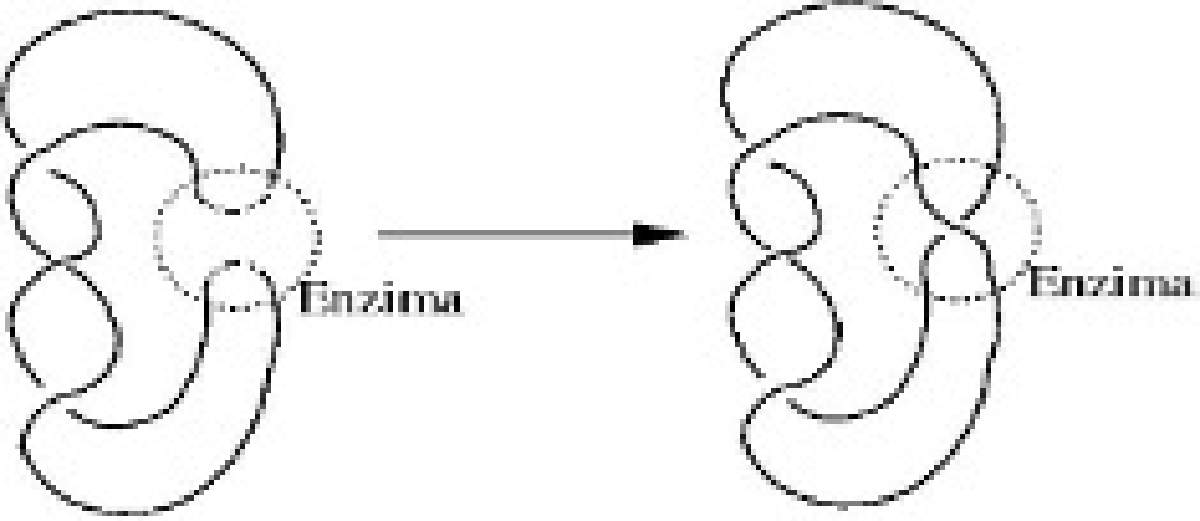
Figura 12. Recombinación en una molécula de ADN
La recombinación sitio-específico está definida como la creación de una nueva secuencia genética a partir de partes de secuencias genéticas existentes, lo cual tiene como consecuencia una manipulación topológica de la molécula de ADN. En el caso que nos ocupa, esta recombinación lleva a la separación de la molécula original en dos piezas circulares cerradas, delimitadas por el sitio de recombinación. Más específicamente, una recombinación sitio-específica es una operación local, cuyo efecto en una molécula de ADN es mover una pieza de esta molécula de ADN a alguna otra posición dentro de ésta misma o importar una pieza de una molécula de ADN distinta en nuestra molécula. Generalmente, estas recombinaciones genéticas introducen nudos o enlaces en las moléculas de ADN.
Para comprender este proceso de recombinación por la acción de enzimas, se ha utilizado teoría de nudos.
Hasta donde sabemos, no hay métodos para observar a las enzimas en acción, pero se pueden observar las moléculas antes y después de que actúen las enzimas, detectar el cambio que se produce y deducir algo sobre la acción de la enzima, modelando este proceso para lo cual se aplican resultados de teoría de nudos.
Referencias
[1] Colin C. Adams. The Knot Book. American Mathematical Society. 2004. https://www.math.cuhk.edu.hk/course_builder/1920/math4900e/Adams--The%20Knot%20Book.pdf
[2] Margareta Boege, Gabriela Hinojosa. Nudos y DNA. Inventio (UAEM), año 2, no. 4 (2006), pags. 41-47. https://inventio.uaem.mx/index.php/inventio/article/view/863/998
[3] Eugenio M. Fedriani Martel & Ángel F. Tenorio Villalón, Los sistemas de numeración maya, azteca e inca, pág. 184. https://web.archive.org/web/20071007195905/http:/www.scm.org.co/Articulos/756.pdf
[4] Kunio Murasugi. Knot Theory and Its Applications. Birkhäuser Boston. 1996. https://www.maths.ed.ac.uk/~v1ranick/papers/murasug3.pdf
[5] Joselyn Soto Contreras. Invariantes polinomiales de nudos. Tesis de Licenciatura, Universidad de Sonora. 2019. https://lic.mat.uson.mx/tesis/joselyn_soto.pdf
Esta columna se prepara y edita semana con semana, en conjunto con investigadores morelenses convencidos del valor del conocimiento científico para el desarrollo social y económico de Morelos.


