El Dr. Mariano López de Haro es investigador del Instituto de Energías Renovables de la Universidad Nacional Autónoma de México, en Temixco, Morelos. Sus áreas de especialidad son la Mecánica Estadística y la Termodinámica de los Procesos Irreversibles. Es miembro fundador de la Academia de Ciencias de Morelos.

Esta publicación fue revisada por el comité editorial de la Academia de Ciencias de Morelos.

Toda persona que trabaje en ciencia aspira a hacer una contribución relevante, que sea recordada como de gran importancia en su campo y, qué mejor, para la ciencia en general. Pero ¿cómo reconocer cuáles son éstas? Es fácil reconocerlas cuando la contribución explica con certeza un aspecto de la naturaleza que intrigaba a las personas investigadoras. Contribuciones como ésas, además de explicar, motivan a otras personas a investigar más e inclusive a desarrollar aplicaciones con un impacto práctico en nuestras vidas.

Pero ¿qué pasa con un trabajo teórico que falla en explicar el fenómeno de interés? ¿Puede ser este trabajo, aunque fallido, tan original que inspire aportaciones posteriores? ¿Puede ocurrir que el propio autor de la contribución original no esté consciente de las ramificaciones de su trabajo? Por sorprendente que parezca, la respuesta a estas preguntas es “sí”. En este artículo, relato la historia de una contribución en una rama de la física conocida como mecánica estadística. La contribución es el Modelo de Ising, y su fascinante historia revela lo intrigante que puede ser la ciencia. Acompáñenme a descubrirla.

El inicio: breves datos de la biografía del autor

Ernst Ising (Figura 1) nació el 10 de mayo de 1900 en Colonia, Alemania. Estudió la secundaria en Bochum y tras un breve lapso de instrucción militar debido a la Primera Guerra Mundial, llevó a cabo estudios de licenciatura en Física, Matemáticas y Astronomía en las Universidades de Gottingen y Bonn, prosiguiendo con un doctorado en Hamburgo, donde se graduó en Ciencias Matemáticas y Naturales con una tesis dirigida por Wilhelm Lenz cuyo título es Beitrag zur Theorie des Ferro- und Paramagnetismus (Contribución a la teoría del ferromagnetismo y el paramagnetismo) en la que aparece su hoy famoso modelo (Figura 2).  Dicha tesis la concluyó el 31 de Julio de 1924, es decir hace poco más de cien años y el modelo sobre el que trabajó, originalmente propuesto por el propio Lenz [1], es precisamente el objeto de esta nota. Cabe señalar que el artículo científico emanado de su tesis con el título Beitrag zur Theorie des Ferromagnetismus fue recibido para publicación el 9 de Diciembre de 1924 y finalmente publicado en el volumen 31 de la revista Zeitschrift für Physik en Febrero de 1925 [2].

Figura 1. Ernst Ising en 1925. Imagen tomada de https://icmp.lviv.ua/ising/books/Ernest_Ising_Brown_University.pdf

Figura 2. Portada de la tesis doctoral de Ernst Ising. Tomada de https://www.scielo.br/j/bjp/a/7psskCZXtFRmYs6fGRrjYkJ/#ModalFigfig02

Después de obtener el grado de doctor, realizó estudios de Filosofía y Pedagogía en la Universidad de Berlin y tuvo diversos trabajos en Alemania en el sector educativo, hasta que, estando ya Adolf Hitler en el poder, perdió forzadamente su empleo primero como servidor público y luego como director de la escuela primaria para niños judíos de Caputh debido precisamente a su origen judío. Llegó incluso a ser interrogado por la Gestapo y en 1939 emigró a Luxemburgo. Cuando los nazis invadieron Luxemburgo, continuaron con la persecución a los judíos y en 1943 Ising tuvo que realizar trabajos forzosos para el ejército alemán, labor que concluyó con la liberación de los aliados. En 1947 emigró a los Estados Unidos y allí trabajó primero en el State Teacher´s College en Minot, North Dakota, y luego como Profesor de Física en la Universidad Bradley en Peoria, Illinois, en la que recibió la distinción de Emérito en 1976. Murió en Peoria el 11 de Mayo de 1998.

Además de su tesis doctoral y el artículo científico asociado a la misma, Ising tiene otra publicación en 1950 en el volumen 18 de la revista American Journal of Physics con el título Goethe as a physicist [3]. En ella, al conmemorarse el bicentenario del nacimiento de Johann Wolfgang Goethe, hace un recuento de algunas contribuciones de Goethe en física, en particular su interés por la óptica y la teoría del color.  Y a pesar de que la teoría del color de Goethe se contraponía a la de Newton y no tuvo éxito, Ising sí le atribuye el nacimiento de una nueva rama de la óptica, la óptica fisiológica.

Las transiciones de fase y el punto crítico

Los conceptos termodinámicos de estados de agregación de la materia (sólido, líquido, gas, plasma) y los cambios de un estado de agregación a otro, se desarrollaron a lo largo del siglo XIX.  En particular, estos conceptos han permitido una descripción   macroscópica (universal)  adecuada de las propiedades de equilibrio asociadas a dichos cambios de estado de agregación independientemente de de la  naturaleza de las sustancias involucradas. Sin embargo,  si uno desea entender a nivel microscópico qué es lo que sucede en los cambios de estado de agregación, es necesario tener en cuenta las características específicas de las interacciones existentes entre las partículas que constituyen dichas sustancias.

Comúnmente la noción de transición de fase se refiere precisamente a cuando una sustancia se transforma de un estado de agregación de la materia a otro. Hay algunas como la fusión (cambio de estado sólido a líquido), la evaporación (cambio de líquido a gas) o la sublimación (cambio de sólido a gas) que tienen asociada una energía o calor latente y en las que el cambio de estado ocurre cuando el sistema absorbe o libera calor sin que cambien la temperatura o la presión. Por ejemplo, cuando se derrite un hielo o al hervir agua. Por otra parte, las transiciones de fase también permiten describir distintos tipos de ordenación magnética.  La más conocida es una transición continua, la transición ferromagnética,  que ocurre en un punto crítico, el llamado punto de Curie. En termodinámica un punto crítico es un punto en el que desaparecen las fronteras entre ambas fases y, por ejemplo en el caso de un fluido,  es el punto terminal de la curva de coexistencia líquido-vapor en equilibrio en un diagrama de presión vs. temperatura. Cabe añadir que las propiedades de un  sistema operando en punto critico son muy diferentes a cuando está operando en la fase ordenada o en la fase desordenada y que el estudio de los puntos y fenómenos críticos  asociados a transiciones continuas con un enfoque microscópico es de gran interés y con plena vigencia e importancia para entender muchos fenómenos que ocurren en sistemas físicos, biológicos, económicos, atmosféricos, etc. Los párrafos siguientes  son precisamente relattivos a un modelo sencillo que tiene que ver con este tema.

El modelo de Lenz-Ising

La rama de la Física en la que yo trabajo, la Mecánica Estadística, tiene como una de sus finalidades la descripción de las propiedades macroscópicas de un sistema a partir del conocimiento de las interacciones de las partículas que lo forman a nivel microscópico. Uno de los enfoques que se sigue es la construcción y consideración de modelos simples, que por una parte capturen las características físicas esenciales y por otra parte permitan el cálculo exacto de algunas propiedades del sistema en cuestión. Y el modelo que nos ocupa en esta nota es precisamente uno de los caballitos de batalla en ese sentido y fue introducido para explicar el ferromagnetismo, fenómeno asociado bien sea al comportamiento intrínseco de un material (como el caso de la magnetita) o a la respuesta que presentan algunos materiales  llamados ferromagnéticos ante la presencia de un campo magnético (por ejemplo el que produce un imán, ver Figura 3).

Figura 3. El campo magnético de un imán en forma de herradura. Tomada de https://www.tiempo.com/noticias/ciencia/sabes-como-funcionan-los-imanes-el-magnetismo-es-la-clave.html

Este comportamiento surge cuando una colección de espines atómicos del material se alinean de forma tal que sus momentos magnéticos apuntan todos en la misma dirección y se genera un momento magnético total macroscópico (ver Glosario). El hierro, el níquel, el cobalto y algunas tierras raras son materiales ferromagnéticos fuertemente atraídos por los imanes y ellos mismos pueden magnetizarse permanentemente. Cabe añadir que, en general, las propiedades magnéticas de estos materiales pueden variar con la temperatura o si se les somete a golpes fuertes. 

El conocido como modelo de Ising, cuyo nombre aparentemente  fue acuñado en un artículo de Rudolph Peierls en 1936 [4] (aunque como el propio Ising reconoció en una carta a S. Kobe en 1994 [5,6] debió llamarse modelo de Lenz-Ising pues como ya apuntamos fue Lenz el de la idea original), consiste en una red de variables de “espín” que pueden tomar únicamente los valores de +1 o -1 y cada par de dichos “espines” (que tienen que ser primeros vecinos) tiene una energía de interacción -E si ambos toman el mismo valor (+1 o -1) y de E si tienen valores distintos. Adicionalmente, un espín puede interaccionar con un campo magnético externo. En la Figura 4 se muestra una representación esquemática del modelo en una, dos y tres dimensiones y su comportamiento a bajas temperaturas (columna izquierda) y a altas temperaturas (columna derecha). Lo que Lenz le propuso a Ising fue que desarrollara en su trabajo doctoral los aspectos matemáticos del modelo que el propio Lenz había propuesto en 1920 para el ferromagnetismo.

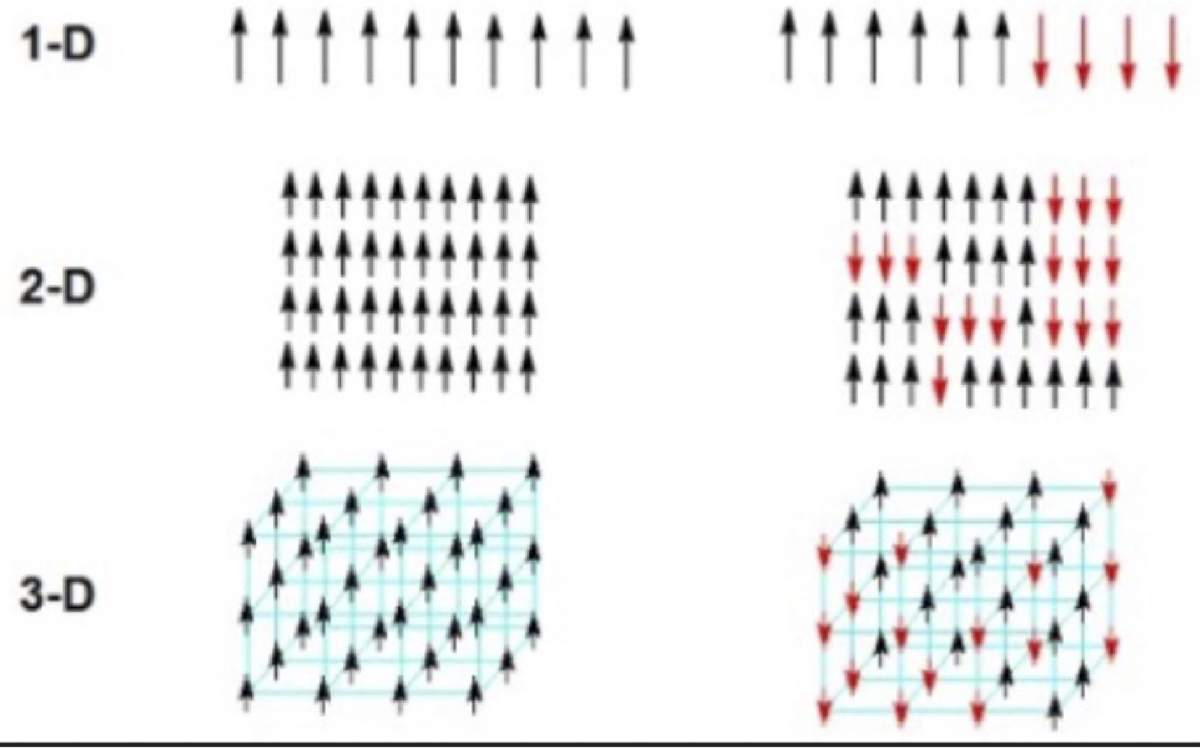
Figura 4. Representación esquemática del modelo de Ising en una, dos y tres dimensiones. La columna izquierda indica el comportamiento a bajas temperaturas y la de la derecha el correspondiente a altas temperaturas.

El modelo unidimensional (en el que los espines forman un anillo) fue resuelto de manera exacta por Ising en su tesis doctoral y el de dos dimensiones (también de forma exacta) por Lars Onsager en 1944 [7], mientras que el de tres dimensiones no ha podido ser resuelto de manera exacta hasta la fecha.

Ising demostró que el modelo unidimensional no podía exhibir ferromagnetismo pero, a partir de este resultado, concluyó erróneamente que en el caso tridimensional ocurriría lo mismo. Esto provocó que el modelo no fuera considerado útil por mucho tiempo. Cabe señalar que Werner Heisenberg [8] fue el primero en citar el trabajo de Ising y, notando sus limitaciones y tomándolas como excusa, aprovechó para desarrollar su propio modelo de ferromagnetismo usando interacciones complicadas entre los espines. Adicionalmente, en el trabajo ya mencionado Peierls demostró que el modelo de Ising en dos y tres dimensiones sí llevaba a una transición de fase (es decir entre pasar de no ser a ser un imán, dependiendo de la temperatura) y señaló la importancia de la dimensión espacial para la presencia en los sistemas de orden de largo alcance y la existencia de una temperatura de transición (en la que el sistema se convierte en un imán) bien definida. También se dio cuenta de la similitud matemática del modelo con otras teorías de fenómenos cooperativos, pero no abundó más en ello. La solución analítica de Onsager para el modelo de Ising bidimensional sirvió para disipar todas las dudas acerca de la validez de la Mecánica Estadística para describir fenómenos críticos y transiciones de fase. El lector interesado puede profundizar en la historia del modelo en las referencias [9], [10] y [11]. Una buena introducción técnica se encuentra en la referencia [12].

Aunque como he señalado, los resultados iniciales del modelo de Ising fueron decepcionantes puesto que no permitía describir la transición ferromagnética (incluso hay que apuntar que el propio Ising se desanimó tanto que dejó la carrera de investigador, aunque no la de docente), basta ver el número de trabajos que lo han citado y utilizado hasta ahora (Figura 5) y los que con toda certeza lo seguirán haciendo en el futuro para darse cuenta de que encierra una riqueza insospechada. De hecho, en el año 2000, S. Kobe señaló que de 1969 a esa fecha dieciséis mil publicaciones habían usado el modelo de Ising. A cien años de su concepción, es uno de los modelos mejor conocidos de la Mecánica Estadística y, con variaciones, se ha empleado no solamente en sistemas magnéticos sino en sistemas tan diversos como los átomos en aleaciones, los vidrios de espín, redes neuronales, problemas de optimización, la evolución del lenguaje, la volatilidad de los mercados financieros, los cambios de humor, las colaboraciones científicas e incluso el uso del suelo y la histéresis asimétrica en la polarización política [13,14].

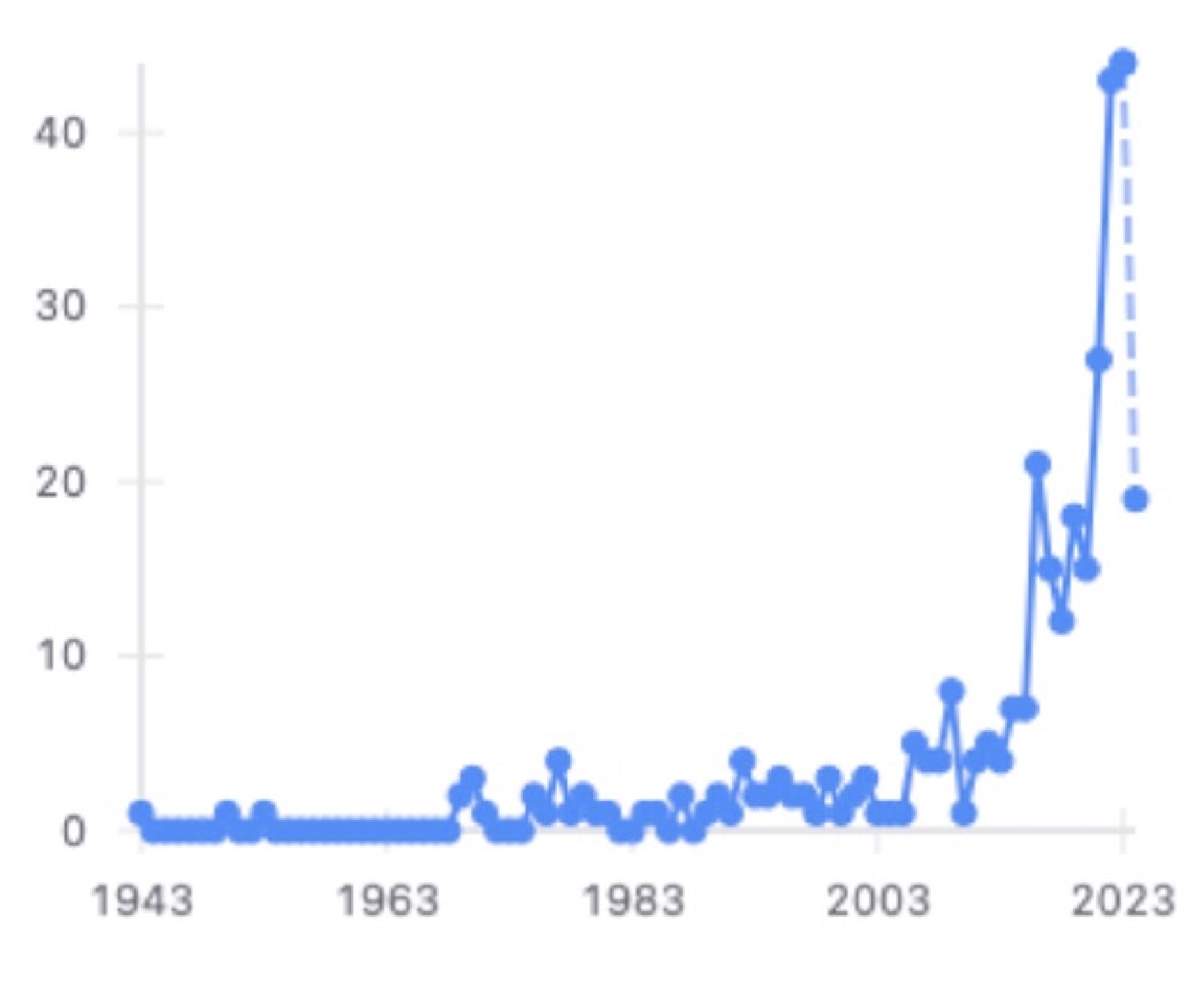
Figura 5. Número de citas al artículo de Ising a través de los años. Los números en el eje vertical están en miles.

En cuanto al impacto del modelo en la ciencia mundial, aún más relevante que el número de citas o el número de trabajos que lo han usado, es el hecho de que varios premios Nobel han sido otorgados a científicos cuyo trabajo estaba inspirado el modelo de Ising. La lista se inició con Chen Ning Yang y Tsung-Dao Lee en 1957, a quienes siguieron Lars Onsager en 1968, Kenneth Wilson en 1982, Thomas Schelling en 2005 y más recientemente Giorgio Parisi en 2021 y John. P. Hopfield en 2024. Es interesante apuntar que Onsager lo recibió en Química, Schelling en Economía y los demás en Física.

Comentarios finales.

La transición de fase más cotidiana es cuando el agua es hielo debajo de 0 grados C y vapor arriba de 100^o C, pero hay otros muchos ejemplos importantísimos en la naturaleza, como la involucrada en el ferromagnetismo. Desde el punto de vista de la Mecánica Estadística, el modelo de Ising nos ayuda a comprender varios aspectos de lo que ocurre en una transición de fase. Además, es uno de los pocos modelos exactamente solubles y que permiten el cálculo explícito y la interpretación de cantidades termodinámicas. Finalmente, se trata de un modelo simple que de manera sorprendente se puede usar para una gran diversidad de sistemas.

No es exagerado afirmar que el modelo de Ising ha sido fundamental en el desarrollo de la Física moderna.  Por ello,  no es extraño que dicho modelo sea  parte de los programas de estudios de la carrera de Física y del posgrado en Física en todas las universidades del mundo. El modelo original  (en una dimensión) de Ising, que iba encaminado al entendimiento de la transición ferromagnética,  fue tan decepcionante  que, como ya señalé,  el mismo Ising no siguió trabajando en él y de hecho abandonó la investigación. Sin embargo, quizás la mayor virtud del modelo de Ising y sus extensiones,  sea que ha ayudado a entender lo que ocurre dentro del sistema en el punto crítico y, por ello, su utilidad no radica tanto en el modelo unidimensional sino en lo que se pudo obtener de él al considerar diferentes dimensiones espaciales (2D, 3D,  y sobre todo mayores a 4D). Así pues, las extensiones y ampliaciones realizadas por otros científicos, y en particular las propiedades de la transición de fase en el punto crítico  que han analizado, sí que han generado un gran desarrollo científico que culminó en grandes avances en diversas áreas.

Finalizo con una traducción libre de un par de párrafos de la nota de Andrea Taroni[15] en Nature Physics, publicada en ocasión de la celebración de los 90 años del modelo y que suscribo totalmente:

“Sin embargo, el verdadero valor del modelo de Ising y sus muchas variantes reside precisamente en la complejidad que encapsulan. Éstas han encontrado utilidad en campos tan diversos como la física de la materia condensada, la química física, las neurociencias y, más ampliamente, el estudio de sistemas complejos.

Ising estudió un modelo decepcionantemente simple que, aunque entonces él no lo sabía, captura la física esencial de una categoría de problemas extremadamente amplia. Él puede haberse equivocado en su artículo de 1925, pero se tropezó sobre una verdadera mina de oro de la física.”

Referencias

1. Lenz, “Beitrag zum Verständnis der magnetischen Erscheinungen in festen Körpern”, Physikalische Zeitschrift 21, 613 (1920).
2. Ising, “Beitrag zur Theorie des Ferromagnetismus”, Zeitschrift für Physik 31, 253 (1925).
3. Ising, “Goethe as a Physicist”, American Journal of Physics 18, 235 (1950).
4. Kobe, “Ernst Ising – Physicist and Teacher”, Journal of Statistical Physics 88, 991 (1997).
5. Kobe, “Ernst Ising 1900-1998”, Brazilian Journal of Physics 40, 649 (2000).
6. Peierls, “On Ising’s model of ferromagnetism”, Proc. Camb. Philos. Soc. 32, 477 (1936).
7. Lars Onsager, “Crystal Statistics. I. A Two-Dimensional Model with an Order-Disorder Transition”, The Physical Review 65, 117 (1944).
8. Heisenberg, “Zur Theorie des Ferromagnetismus”, Zeitschrift für Physik 49, 619 (1928).
9. G. Brush, “History of the Lenz-Ising model”, Rev. Mod. Phys. 39, 883 (1967).
10. Niss, “History of the Lenz-Ising Model 1920–1950: From Ferromagnetic to Cooperative Phenomena”, Arch. Hist. Exact Sci. 59, 267 (2005).
11. Niss, “History of the Lenz-Ising Model 1950–1965: from irrelevance to relevance”, Arch. Hist. Exact Sci. 63, 243 (2009).
12. S. Walker, A student’s guide to the Ising Model (Cambridge University Press, Cambridge, 2023).
13. Budrikis, “100 years of the Ising model”, Nature Reviews Physics 6, 530 (2024).
14. W. Macy, B. K. Szymanski y J. A. Hołyst, “The Ising model celebrates a century of interdisciplinary contributions”, npj Complex1, 10 (2024).
15. Taroni, ”90 years of the Ising model”, Nature Physics 11, 997 (2015).

Esta columna se prepara y edita semana con semana, en conjunto con investigadores morelenses convencidos del valor del conocimiento científico para el desarrollo social y económico de Morelos.